Choosing the Best SDXL Samplers for Image Generation

While playing around with SDXL 1.0 on Segmind, you must have come across a parameter in advanced settings: Scheduler. Perhaps you've pondered the nature of these schedulers, their impact on image generation, and the tradeoffs linked to each. This technical blog aims to delve into an exploration of these schedulers, unraveling their intricacies and shedding light on their effects on the image generation process.

What Exactly Are Schedulers?

Schedulers, often referred to interchangeably with samplers, are specialized algorithms that play a crucial role in the denoising process of the Stable Diffusion pipeline. These algorithms work by repeatedly applying denoising steps to the input data, progressively adding and removing random noise during each iteration. This method leads to a gradual improvement in image quality, resulting in visibly clearer enhanced and cleaner images.

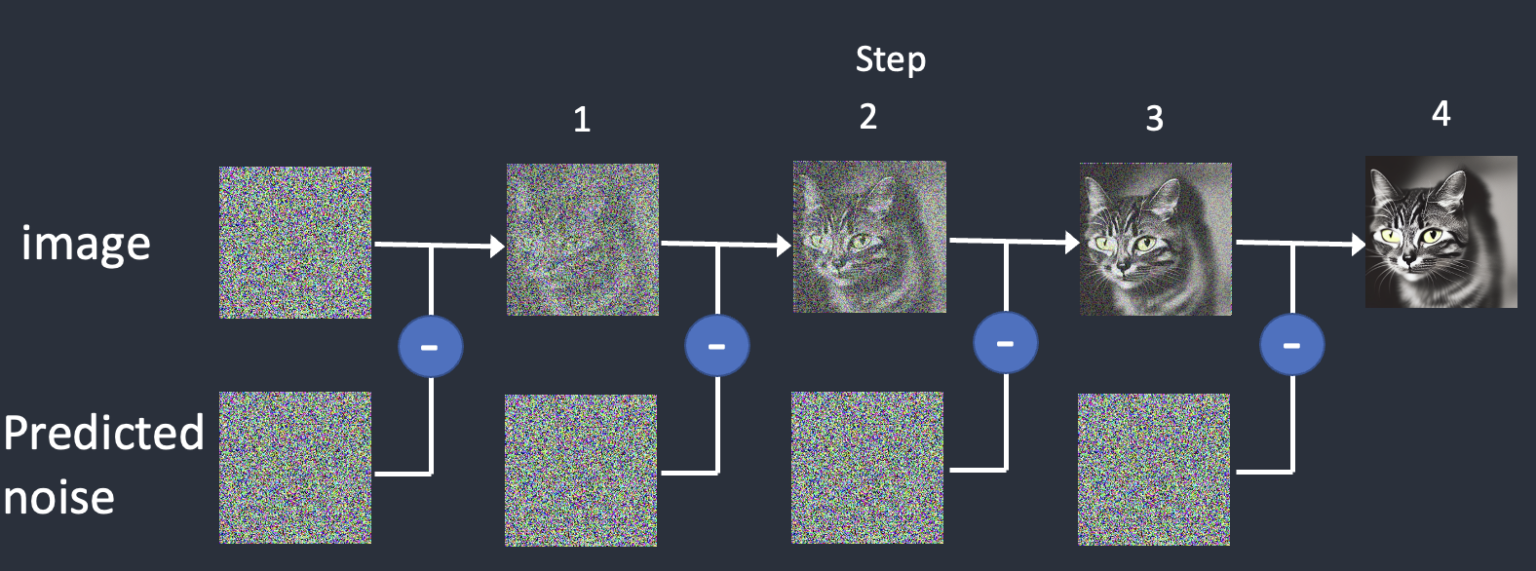
Central to the functioning of samplers is their sampling technique, which entails creating a new sample image at every step of the iteration. This phase significantly contributes to the ultimate result produced by the system.

It's important to note that samplers fall under a broader category of numerical approximation methods engineered to address complex differential equation problems.

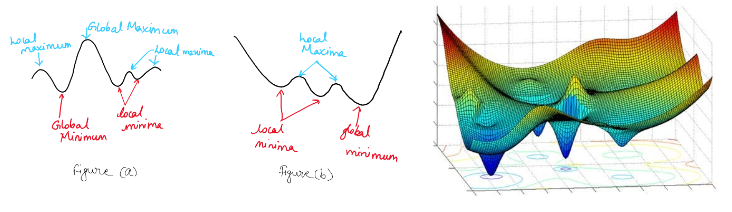
To illustrate, consider trying to find the deepest part of the ocean - an extremely challenging task given the immense scale and intricacy involved. Instead of determining the precise location, one has to resort to estimations based on the current position. Likewise, samplers function as navigational instruments guiding us toward the desired outcome within a sea of myriad choices. Consequently, choosing an effective sampler emerges as vital for achieving satisfactory outcomes.

Schedulers within the Stable Diffusion Pipeline

Working closely with the UNet segment, schedulers manage both the rate of advancement and intensity of noise throughout the diffusion process. As mentioned earlier, schedulers introduce escalating random noise to the data before subsequently reducing it, resulting in improved image clarity over time.

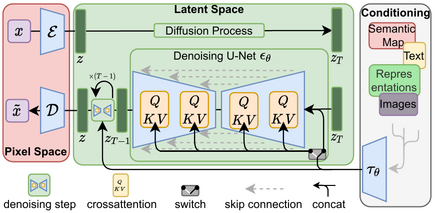
Controlling the pace of alteration and managing noise levels directly influence the ultimate aesthetic qualities displayed by the generated images. Thus, mastery over scheduler selection and configuration proves vital in harnessing the full capabilities offered by the Stable Diffusion pipeline.

As of now on Segmind, users can choose from over ten distinct scheduler types tailored for diverse scenarios. Each option carries unique advantages and tradeoffs depending upon factors such as computational requirements, precision, and processing speeds. Understanding these aspects allows developers to make informed decisions regarding which scheduler aligns best with specific project needs and constraints.

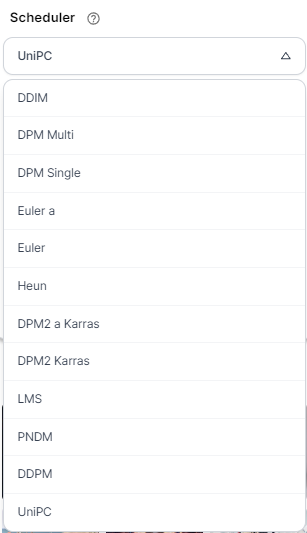
DDPM

DDPM, or Denoising Diffusion Probabilistic Models is one of the first schedulers available in Stable Diffusion. It is a cutting-edge generative model inspired by non-equilibrium thermodynamics. Their distinctive approach combines diffusion probabilistic models with denoising score matching connected to Langevin dynamics, enabling innovative progressive lossy decompression schemes analogous to autoregressive decoding. Leveraging latent variable models, DDPMs gradually eliminate noise from images throughout multiple steps while enhancing sample quality.

Notably, DDPMs excel at generating high-quality images or sounds but demand considerable time and resources due to requiring hundreds to thousands of iterations for producing final samples. This is generally seen as outdated and not longer widely used anymore

DDIM

Based on a paper from Stanford University in 2021, DDIM (Denoising Diffusion Implicit Models) improves upon DDPMs, offering 10x to 50x speed-ups in processing without compromising image quality. Its efficiency lies in implementing an iterative implicit probabilistic model and employing non-Markovian diffusion processes. DDIMs introduce deterministic generative mechanisms, drastically increasing the pace of high-quality sample creation.

Additionally, DDIMs permit flexible trade-offs between computation and sample quality, empower semantically profound image interpolation within latent space, and ensure highly accurate observation restoration with minimal distortion.

PNDM

PNDM (Pseudo Numerical Methods for Diffusion models on Manifolds) improves DDPM's inference process without hurting the quality of generated samples. Thinking of DDPMs as solving differential equations on manifolds, PNDM introduces ways to increase efficiency. A "manifold" is a mathematical space that, on a small scale, looks like Euclidean space of a certain dimension. Navigating these spaces is likened to generating samples using DDPMs. Classical numerical methods for solving differential equations inspire PNDM techniques.

With PNDM, generating high-quality artificial images happens in just 50 steps, unlike older methods such as DDIMs demanding 1000 steps. This means a 20x speedup, retaining original image quality. Therefore, PNDM saves time and conserves quality, ensuring optimal results for varied applications.

Euler

Originating from Nvidia's research, Euler is a fast scheduler using k-diffusion on PyTorch. It requires 20-30 steps for generating high-quality outputs, balancing speed and efficacy. Euler's method is a simple and fast numerical technique for solving ordinary differential equations (ODEs). It estimates solutions by taking small steps along tangent lines of the function being solved. While not always the most accurate, it is widely used due to its simplicity and efficiency.

Euler a

Euler a mixes usual Euler moves with random leaps based on older values, allowing varied ancestral sampling. It manages steady progress towards targets while enabling random detours inspired by past steps, offering plenty of possible setups related to aims. Leveraging ancestral sampling techniques and the Euler method, this scheduler efficiently adjusts step size based on sigma values, enhancing computational efficiency without sacrificing image quality.

Heun

Heun is like Euler's detail-oriented relative. Whereas Euler does merely linear guesswork, Heun carries out two jobs at every step, classifying it as a second-level sampling method. Here's how it operates: initially, it makes a rough projection utilizing linear principles, and afterward, it polishes up said prediction using nonlinear strategies. With this consecutive scheme comprising anticipation plus refinement, Heun regularly yields better outcome accuracy than Euler.

Heun gives more accurate results but needs twice the time, similar to choosing a delicious yet slow-cooked meal over faster, less tasty options.

LMS

The LMS or Linear Multi-Step method, utilized for solving Ordinary Differential Equations (ODEs), varies from Probabilistic Linear Multi-Step ( PLMS) owing to its preference for numerical versus probabilistic approaches (PLMS - P = LMS). Its edge lies in integrating historical data into each step, minimizing noise while delivering greater precision than simpler methods such as Euler and Heun. Yet, there's a trade-off: boosted computational needs lead to slow operation.

Belonging to the wider class of numerical integration techniques targeting ODE resolution, LMS commences at an initial stage, advancing systematically across time whilst computing subsequent answers iteratively. Distinctively different from basic tactics like Euler's method relying on a lone previous point and related derivative, LMS keeps multipoint historical records. Such extensive recall empowers LMS to make far more accurate forecasts than possible through limited recall means alone, rendering it a powerful tool despite its relatively high computational expense.

Family of DPM models

DPM (Diffusion Probabilistic Models) are probabilistic models that offers improvements over DDPM . DPM2 is an improvement over DPM.

DPM (Single & Multi)

Diffusion Probabilistic Models (DPMs) deliver remarkable generation capabilities but struggle with extended sampling periods. Traditional approaches rely heavily on black-box ODE solvers, consuming considerable computation time and resources.

Enter DPM-Solver, designed specifically to tackle the shortcomings of standard ODE solvers found in DPMs. Its key innovation lies in directly computing the primary components of the solution, reducing reliance on generalized ODE solvers. Additionally, DPM-Solver integrates smoothly with established systems via change-of-variable optimizations.

Single-step ("S") and multi-step ("M") solvers are numerical techniques used to estimate solutions for differential equations. Single-step calculates one value per step quickly but has lower precision; multi-step computes multiple values simultaneously based on past data, providing higher precision but slower execution. Factors influencing solver selection include equation complexity, desired accuracy, system stability, and computational capacity. The order of the solver (e.g., 1, 2, 3) indicates the number of previous time steps used in the multi-step solver, with higher orders typically offering improved accuracy. Choose wisely depending on your needs!

DPM2 Karras

The Karras schedule is a minor variation of the conventional schedule that has been observed to perform better through experimentation. DPM2-Karras not only provides fine control over image variations but also emphasizes appearance customization. By offering adjustments for various attributes like color, texture, and style, users can generate images tailored to their preferences or requirements using this advanced denoising diffusion probabilistic model.

DPM2 a Karras

DPM2 a Karras prioritizes diversifying generated content and venturing into unexplored image domains. By focusing on ancestral sampling techniques, this denoising diffusion probabilistic model fosters greater variety and uniqueness in its output images, enabling creative freedom and discovery of previously uncharted visual territories.

UniPC

UniPC is a unified predictor-corrector framework for swift and high-quality sampling across various probabilistic models, comprising a unified predictor (UniP) and a unified corrector (UniC). UniPC adapts to different levels of precision without needing further model calculations, increasing sampling speed and effectiveness, particularly for image synthesis tasks—both unconditional and conditional—using pre-trained models based in pixels or latent spaces.

Demonstrating remarkable progress, the UniPC paper presents a two-component technique—the unified predictor (UniP) and unified corrector (UniC)—targeted towards maximizing sampling quality within minimal steps, applicable to multiple probabilistic models. For instance, PNDM previously diminished required steps to 50 versus DDIM's initial 1000, whereas UniPC generates comparative or improved image quality in just 5-10 steps, marking considerable advancements in probabilistic modeling through mathematics-driven methods promoting accelerated, premier image production.

Best Scheduler?

Is a sailboat or a motorboat better? Depends if you're enjoying the wind's grace or racing against the clock, right? Depending on what you want, it’s better to use one type of scheduler or another.

Generation Speed

When testing prompts, avoiding extended waits for results is preferable. In scenarios where the emphasis is on swift experimentation of changes rather than achieving maximum quality, the recommendation is to use Euler , DPM S or UniPC with a limited number of steps.

Image Quality

If your objective is to attain high quality, it is advisable to aim for convergence. This is the stage where the highest quality is achieved. Heun and LMS can yield favorable outcomes owing to their numerical characteristics. Alternatively, exploring DPM2 Karras and UniPC are also viable options.

Creativity

This segment is specifically designated for ancestral samplers. These samplers distinguish themselves not by delivering subpar quality or sluggish performance but by their distinctiveness. The unique aspect, or challenge (depending on one's perspective), associated with these samplers lies in the fact that achieving an image in 50 steps instead of 40 can result in an improvement or deterioration of the image.

Continuous testing is necessary in order to ascertain the outcome. This unpredictability introduces a creative element to these samplers, as the ability to alter the number of steps allows for obtaining subtle variations. Notably, Euler a and DPM2 a Karras emerge as victorious here

Further Readings:

1. Best settings for Stable Diffusion SDXL 1.0 [Read Here]
2. The ML developers guide to Schedulers in Stable Diffusion [Read Here]